Gear4
A 4th order Rear Method (Backward Differentiation Formulas) solver for stiff intial value problem (IVP)
Syntax for 1st-Order IVP
gear4(dydt, t_start, t_end, nstep, y0) |
Input: dydt is a user defined function of the form dydt(t, y) => {some expression of y and t} t_start is a real number for initial time t_end is a real number of end time nstep is an positive integer implies the preferred time steps for the solutions y0 is a real number for the initial value of y when t = t_start Result: A row vector gives the time points of t for the solutions A column vector gives the solutions y for the time points t. |
gear4(dydt, t_start, t_end, nstep, y0, abserr, relerr) |
Input: dydt is a user defined function of the form dydt(y, t) => {some expression of y and t} t_start is a real number for initial time t_end is a real number of end time nstep is an positive integer implies the preferred time steps for the solutions y0 is a real number for the initial value of y when t = t_start abserr is a real number for absolute tolerance relerr is a real number for relative tolerance Result: A row vector gives the time points of t for the solutions A column vector gives the solutions y for the time points t. |
gear4(dydt, t, y0) |
Input: dydt is a user defined function of the form dydt(y, t) => {some expression of y and t} t is a row/column vector which gives the preferred time points for the solutions y0 is a real number for the initial value of y when t = t[0] Result: A row vector gives the time points of t for the solutions A column vector gives the solutions y for the time points t. |
gear4(dydt, t, y0, abserr, relerr) |
Input: dydt is a user defined function of the form dydt(y, t) => {some expression of y and t} t is a row/column vector which gives the preferred time points for the solutions y0 is a real number for the initial value of y when t = t[0] abserr is a real number for absolute tolerance relerr is a real number for relative tolerance Result: A row vector gives the time points of t for the solutions A column vector gives the solutions y for the time points t. |
Syntax for High-Order IVP
gear4(<dy1dt, ...>, t_start, t_end, nstep, y0) |
Input: <dy1dt, dy2dt, ...> is a group of user defined functions of the form dydt(t, y1, y2, ...) => {some expression of t, y1, y2, ...}, which are enclosed with '<>' . These functions defined the all 1st-order IVP differential equations converted from the high-order ODE. t_start is a real number for initial time t_end is a real number of end time nstep is an positive integer implies the preferred time steps for the solutions y0 is a real number for the initial value of y when t = t_start Result: A row vector gives the time points of t for the solutions A matrix gives the solutions y for the time points t whose first column is solution for y1, second row for y2, etc. |
gear4(<dy1dt, ...>, t_start, t_end, nstep, y0, abserr, relerr) |
Input: <dy1dt, dy2dt, ...> is a group of user defined functions of the form dydt(t, y1, y2, ...) => {some expression of t, y1, y2, ...}, which are enclosed with '<>' . These functions defined the all 1st-order IVP differential equations converted from the high-order ODE. t_start is a real number for initial time t_end is a real number of end time nstep is an positive integer implies the preferred time steps for the solutions y0 is a real number for the initial value of y when t = t_start abserr is a real number for absolute tolerance relerr is a real number for relative tolerance Result: A row vector gives the time points of t for the solutions A matrix gives the solutions y for the time points t whose first column is solution for y1, second row for y2, etc. |
gear4(<dy1dt, ...>, t, y0) |
Input: <dy1dt, dy2dt, ...> is a group of user defined functions of the form dydt(t, y1, y2, ...) => {some expression of t, y1, y2, ...}, which are enclosed with '<>' . These functions defined the all 1st-order IVP differential equations converted from the high-order ODE. t is a row/column vector which gives the preferred time points for the solutions y0 is a real number for the initial value of y when t = t[0] Result: A row vector gives the time points of t for the solutions A matrix gives the solutions y for the time points t whose first column is solution for y1, second row for y2, etc. |
gear4(<dy1dt, ...>, t, y0, abserr, relerr) |
Input: <dy1dt, dy2dt, ...> is a group of user defined functions of the form dydt(t, y1, y2, ...) => {some expression of t, y1, y2, ...}, which are enclosed with '<>' . These functions defined the all 1st-order IVP differential equations converted from the high-order ODE. t is a row/column vector which gives the preferred time points for the solutions y0 is a real number for the initial value of y when t = t[0] abserr is a real number for absolute tolerance relerr is a real number for relative tolerance Result: A row vector gives the time points of t for the solutions A matrix gives the solutions y for the time points t whose first column is solution for y1, second row for y2, etc. |
Example
Solve Problem
y1' = y2
y2' = -10000 * y1 + (-10001) * y2
y1(0) = 1
y2(0) = -1
between the time [0,20].
Input |
Output |
dy1dt(t, y1, y2) => y2 dy2dt(t, y1, y2) => -10000 * y1 + (-10001) * y2 gear4(<dy1dt, dy2dt>, 0, 20, 20, [1, -1]) |
|
Discussion:
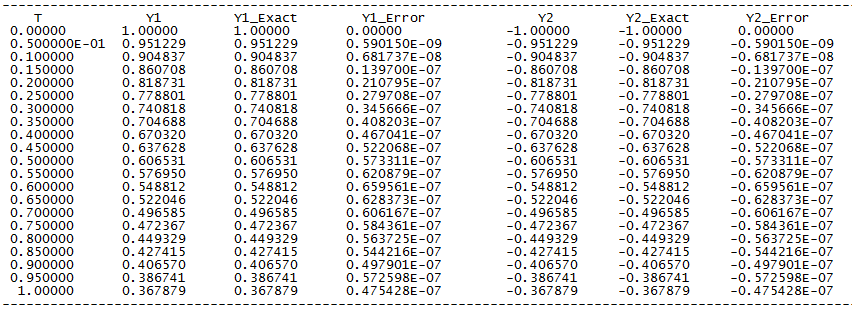
Problem has an exact solution of
y1(t) = exp(-t)
y2(t) = -exp(-t)
Compare the numerical solution above with the exact solution you get
See Also
Created with the Personal Edition of HelpNDoc: Easily create PDF Help documents